|
Size: 3937
Comment:
|
Size: 3933
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| Line 4: | Line 3: |
| Line 8: | Line 6: |
| Line 23: | Line 22: |
| When we do normal single particle analysis, each particle already has (at least) 5 values associated with it: the x-y shift needed to center the particle and the 3 Euler angles defining it's 3-D orientation. The goal of manifold methods is to associate several additional numbers with each particle, each associated with some particular, possibly independent, motion of the system. If | When we do normal single particle analysis, each particle already has (at least) 5 values associated with it: the x-y shift needed to center the particle and the 3 Euler angles defining it's 3-D orientation. The goal of manifold methods is to associate several additional numbers with each particle, each associated with some particular, possibly independent, motion of the system. If |
| Line 26: | Line 25: |
| [[attachment:figure1.jpg]] | {{attachment:figure1.jpg}} |
| Line 29: | Line 28: |
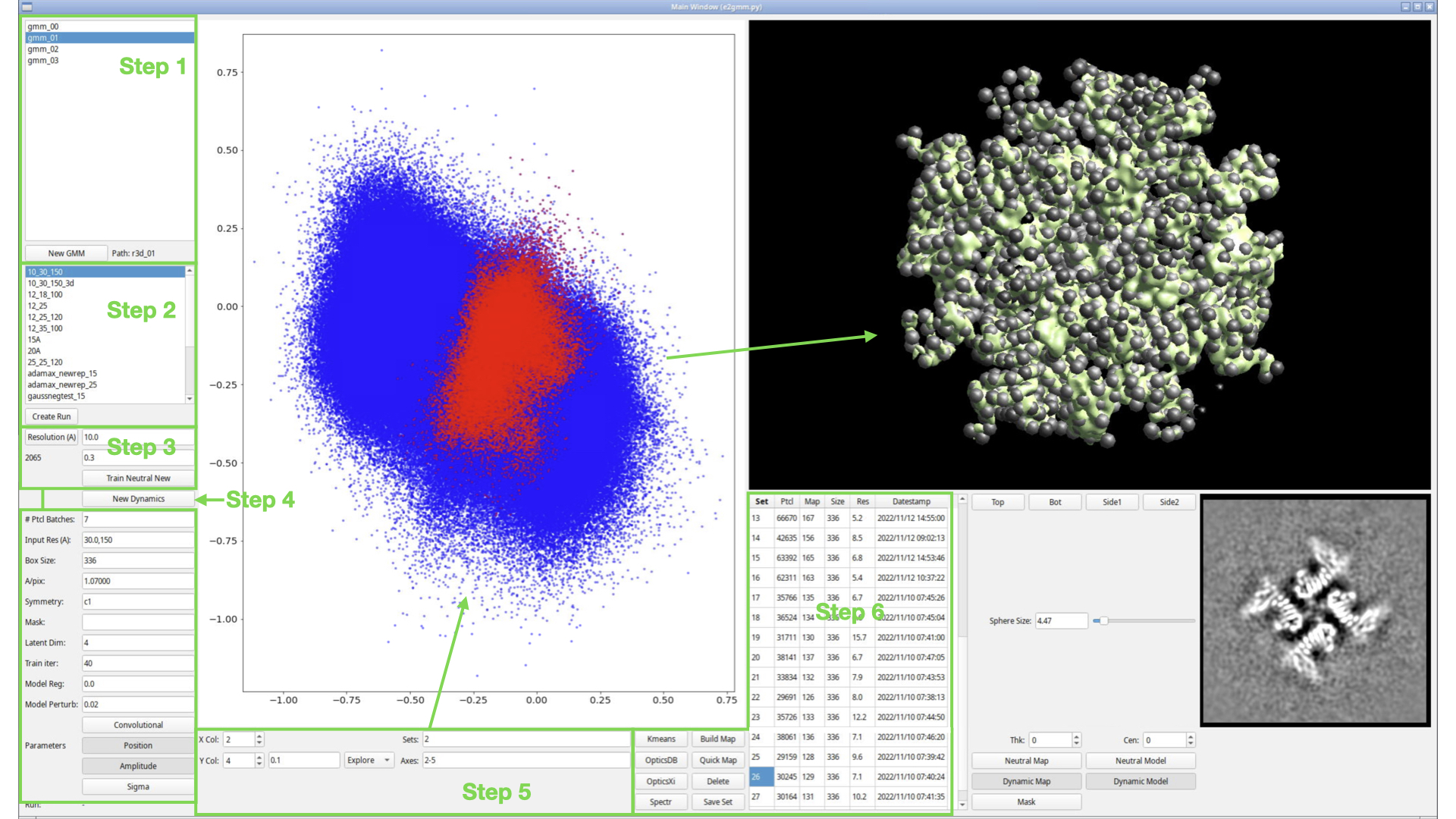
| In step 1, we select an existing refinement run to use as a starting point for the GMM. | In step 1, we select an existing refinement run to use as a starting point for the GMM. |
THIS PAGE IS UNDER CONSTRUCTION
e2gmm - A semi-friendly GUI for running GMM dynamics in EMAN2
This tutorial discusses the new (2022) GUI tool for making use of the Gaussian Mixture Model based variability tools in EMAN2. These tools are still under development, but are now in a usable form. With the GUI these tools are more approachable for typical CryoEM/ET investigators. We recommend this as a good starting point for understanding the method even if you plan to use command line tools manually in the end.
First, a quick overview of the programs:
e2gmm.py - A graphical interface for GMM analysis of single particle or subtomogram averaging data sets. Makes use of e2gmm_refine_point.py
e2gmm_refine.py - The original GMM program as described in the first GMM paper (PMC8363932), largely superseded now
e2gmm_refine_point.py - Dr. Ludtke's new variant, used by the GUI. Significant mathematical changes from the original, but requires substantially less RAM, and in many cases produces better particle classification
e2gmm_refine_new.py - Dr. Chen's new variant, where he is exploring new refinement methods. He is developing a separate tutorial for this new tool.
e2gmm_analysis.py - Ancillary program used to analyze the output of GMM runs. Related functionality to some of the GUI tools.
This tutorial covers e2gmm.py, the GUI interface, which currently makes use of e2gmm_refine_point.py.
Quick Theory Overview
e2gmm is one of several emerging tools in the CryoEM community which make use of a mathematical concept known as manifold embedding to characterize the compositional and conformational variability of a macromolecular system. So, what does that mean, exactly? The concept is not as complicated or intimidating as it may sound. If you think about a large biomolecule in solution, it should be obvious that the picture of a single absolutely static high resolution structure simply does not reflect reality. At the very least, the structure is being continuously impacted by solvent molecules causing motion at least on the level of individual atoms or side-chains. However, for the vast majority of biomolecules it goes far beyond this, with large domain scale motions and assembly/disassembly processes going on continuously as part of the macromolecular function.
Why then are most macromolecules represented in the PDB as "the high resolution structure of X"? This really came from X-ray crystallography where, to solve the structure, the molecules have to be identically configured, and packed into a crystal lattice. However, this concept has now been extended to CryoEM, where practitioners routinely discard 90% of their raw particle data to achieve "the high resolution structure of X". In CryoEM, the next step beyond this, towards reality, are the traditional classification approaches, where a large heterogeneous data set is classified into N more homogeneous subsets, which are then processed (often again discarding large portions of the subset) to produce "N high resolution structures of X". Clearly this is an improvement, and is a reasonable way to represent discrete events such as association/dissociation/ligand binding, but still won't adequately capture continuous changes from state A to state B.
If
When we do normal single particle analysis, each particle already has (at least) 5 values associated with it: the x-y shift needed to center the particle and the 3 Euler angles defining it's 3-D orientation. The goal of manifold methods is to associate several additional numbers with each particle, each associated with some particular, possibly independent, motion of the system. If
Getting Started
Step 1
In step 1, we select an existing refinement run to use as a starting point for the GMM.
