|
Size: 3937
Comment:
|
← Revision 15 as of 2022-12-05 14:00:10 ⇥
Size: 24062
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| * '''TODO - indicates incomplete tutorial sections''' * '''THE e2gmm program is under active development. STRONGLY encourage using an EMAN2 snapshot or source version dated 12/2022 or later. Even with a current version you may notice some small differences in the display, etc.''' * '''This makes extensive use of tensorflow, and the training even on a GPU can, in some cases, take several hours. This tutorial is intended to be run on a Linux box with an NVidia GPU.''' |
|
| Line 4: | Line 7: |
| Line 8: | Line 10: |
| Line 21: | Line 24: |
| If When we do normal single particle analysis, each particle already has (at least) 5 values associated with it: the x-y shift needed to center the particle and the 3 Euler angles defining it's 3-D orientation. The goal of manifold methods is to associate several additional numbers with each particle, each associated with some particular, possibly independent, motion of the system. If |
When we do normal single particle analysis, each particle already has (at least) 5 values associated with it: the x-y shift needed to center the particle and the 3 Euler angles defining it's 3-D orientation. The goal of manifold methods is to associate several additional numbers with each particle, each associated with some particular, possibly independent, motion of the system. If (TODO) |
| Line 26: | Line 28: |
| [[attachment:figure1.jpg]] | {{attachment:figure1.jpg}} The GMM requires a set of single particle or subtomogram averaging data to use as input. It also requires particle orientations, generally determined with respect to a single "neutral" structure. In step 1, we create a gmm_XX folder, which is attached to a specific existing refinement run (refine_XX, r3d_XX or spt_XX). At the moment if you want to work with a Relion refinement, you will need to import the STAR file into an EMAN2 project first, then open the resulting folder (TODO). For this tutorial we suggest using the results of the [[EMAN2/e2TomoSmall|Subtomogram Averaging Tutorial]] as the starting point for this tutorial. The single particle tutorial uses beta-galactosidase, which has minimal flexibility and high symmetry, and isn't really suitable for the GMM. The subtomogram averaging tutorial, however, uses ribosomes, which exhibits a clear ratcheting motion and generally has a subset of "bad" particles. |
| Line 29: | Line 35: |
| In step 1, we select an existing refinement run to use as a starting point for the GMM. | Press the "New GMM" button, select one of the supported folder types, and press OK. There will be a moderate delay after pressing OK while the GMM folder is constructed and populated. ==== Step 2 ==== The dynamics/variability in a complex macromolecule becomes more and more complicated, with more and more degrees of freedom as you increase the level of detail. At the extreme, you could consider the anisotropic motions of the individual atoms as reflected in crystallography by anisotropic B-factors. But even taking a step back from that, most sidechains in solution are almost certainly not rigidly oriented. With this in mind, when looking at dynamics, it is important to consider the lengthscale you wish to consider. Normally, it would make sense to start with the coarsest lengthscales and look for large scale motions like the racheting mechanism in the ribosome or the association/dissociation of components of the macromolecular system. If those are characterized and understood (or do not exist in a significant way), then moving down to examine domain motions, then motions of individual secondary structures, etc. makes sense. So, while the GMM tool is automated, the user still has to make decisions about the level of detail to explore, how many degrees of freedom to permit, whether to focus the analysis using a mask, etc. That is, you will almost certainly want to do more than one run of the GMM system with different parameters as part of your explorations. In step 2, we create (named) GMM runs. Each run will have its own set of parameters, and will exist in the context of the selected GMM_XX folder from Step 1. * Press '''Create Run''' * Enter "15_25_100" * Press Enter or click '''OK''' You may use whatever name you like for these runs, BUT the name will be used as part of the filename of several files, so please do not include spaces or special characters other than "_","-" or "+" in the name. You may also consider keeping the name relatively short. Depending on the version you are running, you may see various warning messages appear in the console after creating your new run. These can be safely ignored if present. You should see an entry for your newly created run appear in the box shown under Step 2. Make sure this new entry is selected. ==== Step 3 ==== In Step 3 we create the neutral Gaussian representation for our neutral map. The "neutral map" represents the solved structure from the folder selected in step 1. It's the map produced when you include all or most of the particles in the data set, and should be a sort of average structure for the system. When we look for dynamics/variability, it will be with respect to this neutral map. To proceed with the GMM, we need to have a Gaussian model for this neutral map. This can be generated automatically, but the user needs to provide two key parameters: 1) the level of detail at which to make the representation and 2) how strong densities need to be to be included in the representation. Item 1) is defined as a resolution (in Å), but do not confuse this with the resolution you might achieve in final classified maps. This number defines the resolution level at which variability will be studied. If you specify 30 Å here, it will be looking for changes/motions in features with a 30 Å lengthscale, but successfully isolating a more self-consistent set of particles could still readily achieve near atomic resolution maps. When starting with a new project we suggest beginning with 20-30 Å here, then if no useful variability is detected, or when you are ready to look for finer motions, then reduce the number incrementally by ~2x. You will want to make a new run (step 2) each time you try new parameters. Item 2) specifies a relative amplitude threshold for Gaussian modeling. This is specified as a resolution-dependent threshold. Larger values -> fewer Gaussians. If there are highly dynamic regions of the structure, specifying too high a threshold may fail to produce any Gaussians in these weaker regions of the map, which will make them less likely to be characterized when training the GMM. Still, there is a balance, as a very large number of Gaussians may be difficult to train, will make the GMM run for a long time, and make the results more difficult to interpret. We suggest selecting a threshold value to produce the fewest Gaussians which seem to include at least some representation of all regions of the map. * '''Resolution''' -> 15 * '''(box below Resolution)''' -> 0.5,0.7 * press '''Resolution''' You should see your neutral map shown in the panel on the right, with some number of spheres visible inside it. The number appearing below the '''Resolution''' button is the number of Gaussians in the current model. You can drag the '''Sphere Size''' slider to adjust the visual size of the spheres. This has no impact on any computations, it is purely for visualization. There is one additional complexity. In addition to producing Gaussians representing the strongest densities in the map, a smaller number of Gaussians representing the strongest negative features in the map (relative to the solvent) will also be produced. These are generally placed in residual CTF artifacts or otherwise just outside the structure, and are useful in accurately characterizing individual particles. If '''(box below Resolution)''' is specified as a single value, a reasonable automatic value is selected for the negative threshold. Optionally, '''(box below resolution)''' can be specified as a comma-separated pair, with the first number as the threshold for positive Gaussians and the second number for negative Gaussians. If the second value is larger, fewer negative Gaussians will be created. If you look at the console after pressing '''Resolution''', you should see an output like "pos: 244", "neg: 38", indicating that the model has 192 positive Gaussians and 46 negative Gaussians. You can play with the parameters above and press '''Resolution''' again as many times as you like to achieve a representation you are happy with, but note that large numbers of Gaussians (>1000) may significantly increase the amount of time required to train the GMM and will increase the GPU memory requirements for the network, and in most cases won't actually accomplish anything useful, unless you are using a large number of latent dimensions. Indeed, useful results can sometimes be obtained with as few as 20 - 30 Gaussians. A few hundred is a reasonable target for typical projects. Once the neutral Gaussian model has been defined, the neural network needs to be initialized. It's critical that the network initialization use parameters compatible with the final GMM training, so we fill these in now: * '''Input Res''' -> 25,150 * '''Mask''' -> nothing, clear the box * '''Latent Dim''' -> 4 * '''Train Iter''' -> 30 * '''Model Reg''' -> 0 * '''Model Perturb''' -> 0.25 * '''Position''' -> selected * '''Amplitude''' -> selected * Press '''Train Neutral''' A number of these parameters can actually be altered for the actual dynamics run, the ones which absolutely cannot be changed without rerunning '''Train Neutral''' are: '''Latent Dim''', '''Mask''' and the selection state of '''Position''' and '''Amplitude'''. If you change any of these, you will need to repeat all of Step 3 before '''Train GMM'''. ==== Step 4 ==== We are now on to the actual network training, where the network learns the variabilities present in the system and tries to establish a reduced dimensionality model covering the most important variations among the data. Unlike linear methods like principal component analysis or normal modes, the model changes represented by different axes in latent space can be quite complicated and the axes are not orthogonal in any meaningful way. That is simply to say that a 4-D latent space can potentially represent far more structural variation than 4-D PCA analysis. For runs using >100,000 particles at typical 10-20 Å resolutions, or smaller numbers of particles at higher resolutions, the particle data itself can require too much memory to train the network all at once. The '''# Ptcl Batches''' field selects how many batches to divide the particle data into for training. Breaking the data into batches requires a certain amount of additional overhead, and total runtime for training the network may be significantly longer than if run as a single batch. A reasonable value will be filled in automatically based on the number of particles in the project, but if you are targeting high resolution variations, and get error messages about memory exhaustion when trying to train the network, increasing the number of batches is a quick way to reduce memory requirements. Conversely if you have a setup with 48 GB of GPU RAM on one effective GPU, you may be able to decrease the number of batches to 1 for larger projects. * press '''Train GMM''' ('''New Dynamics''' in older snapshots) * How long this takes to run will depend on quite a few parameters, including the number of particles (for tomographic data, think number of particles*number of tilts), number of Gaussians, Training Iterations, speed of GPU, etc. You can monitor progress in the console. Note that the main refinement program will be run 3*batches times. ==== Step 5 ==== When the GMM finishes training (may be 20 minutes or hours), a scatter plot should appear in the central panel on the display. The GMM will convert each particle image in the data set into a point in the N dimensional latent space (we selected 3 dimensions above, but 4 or 5 would be more typical). In turn, each point in the latent space represents a complete 3-D configuration of the GMM. That is to say, that ostensibly, each particle now has a complete 3-D representation in terms of Gaussians. In reality, since the particles are quite noisy, the individual particles will not be positioned at exactly the optimal point in the latent space, but if we take a set of particles and average their latent space coordinates, the resulting Gaussian model should be a good match for the 3-D reconstruction which would be produced from the corresponding particles. Again, it is difficult to represent 4 or 5 dimensional points in a useful way on 2-D plot window in the middle of the display. The simplest approach is used here, the plot will show a 2-D projection of the N-dim latent space. Using '''X Col''' and '''Y Col''' you can select which dimensions correspond to the X and Y axes in the plot. Furthermore, the program automatically runs PCA on the latent space as soon as the run is complete, and axes 0 and 1 (the default axes shown in the plot) represent a projection defined by the first 2 Eigenvectors of the PCA. Columns 2-N+1 contain the raw latent space axes. It is also possible through external programs to perform other dimensionality reduction algorithms and include the transformed coordinates as additional columns in the plot (advanced topic for later). Dragging the mouse around in the latent space will show crosshairs with a circle. All of the points within the circle will be used to compute the Latent space location, which will then be used to update the pattern of Gaussians in the window on the right in real-time. The box to the left of '''Explore''' controls the radius of the circle. Note again, that the 2-D plot is showing a projection of an N-dimensional space, and any other dimensions will be unconstrained as you drag. ie - you are not extracting points within a 2-D circle, but an N-D hyperslab. The 3-D view on the right can display quite a few different things. The panel of toggle buttons: '''Neutral Map''', '''Neutral Model''', '''Dynamic Map''', '''Dynamic Model''', '''Mask''', gives one way to turn on and off the various components of the display. As usual you can also middle click on the display to open it's control panel and alter the display that way. Note that you can develop some synchronization issues between the various buttons when doing this, so sometimes you may need to turn an item off then on again or vice-versa to get things in sync again. * Turn off '''Neutral Map''' and '''Neutral Model'''. Make sure '''Dynamic Model''' is enabled. You don't have any '''Dynamic Maps''' yet, so that doesn't matter. * Drag your mouse around the plot and observe changes. * Change '''X Col''' and '''Y Col''' and observe the different projections. * By rotating the 3-D view you should be able to identify how specific Gaussian motions relate to specific features in the latent space. ==== Step 6 ==== The next step is to generate maps from subsets of the particles. While these sets can be generated with the mouse, the resulting hyperslabs aren't generally as interesting as classes resulting from N-dim classification. * '''Sets''' -> 8 * '''Axes''' -> 2-5 (make sure you don't use numbers outside the range of available dimensions, remember 0,1 are a PCA projection) * press '''Kmeans''' You should see a list of 8 entries appear in the table below the 3-D view. Clicking on any one of these entries will highlight the corresponding points (again, each point represents a particle) and update the Gaussian model for those points. You can alter '''X Col''' and '''Y Col''' to observe that this classification is truly N-dimensional, not limited to a particular plane. You can select multiple entries at once, and each will be displayed in a different color. Note that the point size in the plot is increased when doing this to make classes easier to see. * Select all of the sets in the list by dragging * Press '''Quick Map''' or '''Build Map''' '''Build Map''' will perform a 3-D reconstruction for all of the particles in each selected set. '''Quick Map''' does the same thing, but downsamples the data by 2x first, making the process run about 8x faster, but limiting the maximum resolution of the map. The reconstructions are performed in the background using multiple threads (look at the console to monitor progress). As each reconstruction completes, the table will be updated. Note that the maps are reconstructed simultaneously, so if you reconstruct 20 maps at the same time, and each map is, say, 512 x 512 x 512, it may use ~20 GB of RAM. '''Quick Map''' will use 1/8 as much, and reducing the number of reconstructions you do simultaneously will also reduce requirements. * Once done, selecting one of the sets in the list will now also display the corresponding map in the 3-D view (the '''Dynamic Map'''). * Furthermore, a central section of the map will be shown in a new window appearing in the lower right side of the display. * The thickness and center of this section can be adjusted with '''Thk:''' and '''Cen:'''. * The orientation of the section follows the orientation of the 3-D view. * Try switching between different sets in different orientations to observe the corresponding differences in 3-D and 2-D. ==== Improving results ==== Notes on training parameters: * '''Input Res''' - This specifies the resolution range which is used to convert individual particles into a set of Gaussian amplitudes. The second number is optional, and if not specified, the full low resolution data is included. Since SSNR is lower at higher resolution, including high resolution in this calculation may lead to each particle being 'noisier' resulting in a less precise position in the latent space. Usually the learned dynamics of the system will still be fine, but it will be hard to relate observed dynamics back to distributions of individual particles. Even relatively small motions will often be measurable at significantly lower resolutions. For example if a domain moves cohesively by only 10 Å, this will still be observable as a change in intensity at 25 Å. So, if you train the GMM and find that significant motions have been identified, but the pattern of particles in latent space (see step 4) seems to be featureless, you may consider increasing the first number. If the GMM seems to be focusing on things like ice gradients or other unimportant very low resolution features, decreasing the second parameter may be worthwhile. * '''Mask''' - Note that we are still considering other ways to handle this parameter, so its behavior may change in future versions. The '''Mask''' parameter allows you to focus the variability analysis on Gaussians within a masked region. The remaining Gaussians will still be present in the model, but will be fixed. When exploring the latent space, only the Gaussians in the masked region should change. However, when generating 3-D reconstructions from the corresponding particles any other coordinated motions should also be observed. Note that masks do not have to be fully connected, so this should be usable to look for coordinated changes between specific disconnected domains. * '''Latent Dim''' - As explained above, there is not a direct relationship between the number of dimensions in the latent space and the 'features' in the model due to the nonlinearity of the network. For looking at the overall motions of most systems 4 is a good choice. While reducing this to 2 or 3 makes visualization easier, and might be an alternative to later dimensional reduction steps, it may also make the network more difficult to train by being too restrictive. * '''Train Iter''' - This may require some trial and error, but generally something between 20 and 100 is a good choice. Note that runtimes will scale linearly with this parameter. In deep learning terms this is the number of 'epochs'. In many cases good convergence can be achieved after 20-30, but if good results are not being obtained, experimenting with larger values may be a good idea. At present, there is no way to continue an existing training session in the GUI, but this may be added soon (so insufficient training can be picked up where it left off). * '''Model Reg''' - If the training seems to drift too far from the starting model due to high noise levels, this regularizer can reduce this phenomenon with a weak restoring force towards the neutral model. If used, suggested values to try might be 0.1 - 0.2. * '''Model Perturb''' - The network training needs to be seeded with a certain amount of entropy to train well in most cases. Larger perturbations will lead to less ordering in the latent space patterns. Usually you would like this value to be as small as possible as long as good training results are achieved. The default value of 0.05 will work well in many cases, but with subtomogram averaging, sometimes stronger perturbations will be required. Generally this number shouldn't be larger than ~0.3, with 1.0 as an absolute maximum. |
THIS PAGE IS UNDER CONSTRUCTION
TODO - indicates incomplete tutorial sections
THE e2gmm program is under active development. STRONGLY encourage using an EMAN2 snapshot or source version dated 12/2022 or later. Even with a current version you may notice some small differences in the display, etc.
This makes extensive use of tensorflow, and the training even on a GPU can, in some cases, take several hours. This tutorial is intended to be run on a Linux box with an NVidia GPU.
e2gmm - A semi-friendly GUI for running GMM dynamics in EMAN2
This tutorial discusses the new (2022) GUI tool for making use of the Gaussian Mixture Model based variability tools in EMAN2. These tools are still under development, but are now in a usable form. With the GUI these tools are more approachable for typical CryoEM/ET investigators. We recommend this as a good starting point for understanding the method even if you plan to use command line tools manually in the end.
First, a quick overview of the programs:
e2gmm.py - A graphical interface for GMM analysis of single particle or subtomogram averaging data sets. Makes use of e2gmm_refine_point.py
e2gmm_refine.py - The original GMM program as described in the first GMM paper (PMC8363932), largely superseded now
e2gmm_refine_point.py - Dr. Ludtke's new variant, used by the GUI. Significant mathematical changes from the original, but requires substantially less RAM, and in many cases produces better particle classification
e2gmm_refine_new.py - Dr. Chen's new variant, where he is exploring new refinement methods. He is developing a separate tutorial for this new tool.
e2gmm_analysis.py - Ancillary program used to analyze the output of GMM runs. Related functionality to some of the GUI tools.
This tutorial covers e2gmm.py, the GUI interface, which currently makes use of e2gmm_refine_point.py.
Quick Theory Overview
e2gmm is one of several emerging tools in the CryoEM community which make use of a mathematical concept known as manifold embedding to characterize the compositional and conformational variability of a macromolecular system. So, what does that mean, exactly? The concept is not as complicated or intimidating as it may sound. If you think about a large biomolecule in solution, it should be obvious that the picture of a single absolutely static high resolution structure simply does not reflect reality. At the very least, the structure is being continuously impacted by solvent molecules causing motion at least on the level of individual atoms or side-chains. However, for the vast majority of biomolecules it goes far beyond this, with large domain scale motions and assembly/disassembly processes going on continuously as part of the macromolecular function.
Why then are most macromolecules represented in the PDB as "the high resolution structure of X"? This really came from X-ray crystallography where, to solve the structure, the molecules have to be identically configured, and packed into a crystal lattice. However, this concept has now been extended to CryoEM, where practitioners routinely discard 90% of their raw particle data to achieve "the high resolution structure of X". In CryoEM, the next step beyond this, towards reality, are the traditional classification approaches, where a large heterogeneous data set is classified into N more homogeneous subsets, which are then processed (often again discarding large portions of the subset) to produce "N high resolution structures of X". Clearly this is an improvement, and is a reasonable way to represent discrete events such as association/dissociation/ligand binding, but still won't adequately capture continuous changes from state A to state B.
When we do normal single particle analysis, each particle already has (at least) 5 values associated with it: the x-y shift needed to center the particle and the 3 Euler angles defining it's 3-D orientation. The goal of manifold methods is to associate several additional numbers with each particle, each associated with some particular, possibly independent, motion of the system. If (TODO)
Getting Started
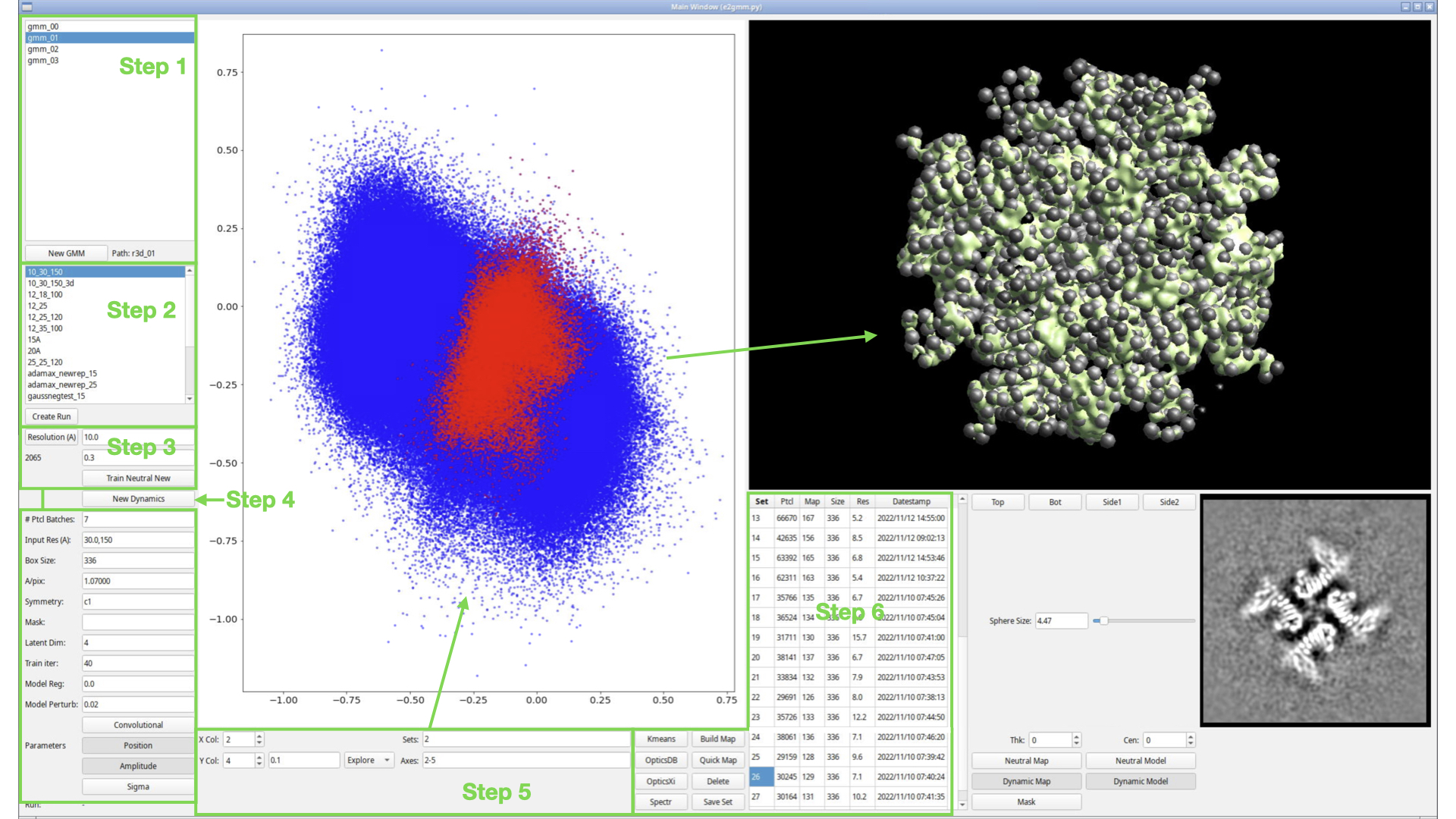
The GMM requires a set of single particle or subtomogram averaging data to use as input. It also requires particle orientations, generally determined with respect to a single "neutral" structure. In step 1, we create a gmm_XX folder, which is attached to a specific existing refinement run (refine_XX, r3d_XX or spt_XX). At the moment if you want to work with a Relion refinement, you will need to import the STAR file into an EMAN2 project first, then open the resulting folder (TODO).
For this tutorial we suggest using the results of the Subtomogram Averaging Tutorial as the starting point for this tutorial. The single particle tutorial uses beta-galactosidase, which has minimal flexibility and high symmetry, and isn't really suitable for the GMM. The subtomogram averaging tutorial, however, uses ribosomes, which exhibits a clear ratcheting motion and generally has a subset of "bad" particles.
Step 1
Press the "New GMM" button, select one of the supported folder types, and press OK. There will be a moderate delay after pressing OK while the GMM folder is constructed and populated.
Step 2
The dynamics/variability in a complex macromolecule becomes more and more complicated, with more and more degrees of freedom as you increase the level of detail. At the extreme, you could consider the anisotropic motions of the individual atoms as reflected in crystallography by anisotropic B-factors. But even taking a step back from that, most sidechains in solution are almost certainly not rigidly oriented. With this in mind, when looking at dynamics, it is important to consider the lengthscale you wish to consider. Normally, it would make sense to start with the coarsest lengthscales and look for large scale motions like the racheting mechanism in the ribosome or the association/dissociation of components of the macromolecular system. If those are characterized and understood (or do not exist in a significant way), then moving down to examine domain motions, then motions of individual secondary structures, etc. makes sense.
So, while the GMM tool is automated, the user still has to make decisions about the level of detail to explore, how many degrees of freedom to permit, whether to focus the analysis using a mask, etc. That is, you will almost certainly want to do more than one run of the GMM system with different parameters as part of your explorations.
In step 2, we create (named) GMM runs. Each run will have its own set of parameters, and will exist in the context of the selected GMM_XX folder from Step 1.
Press Create Run
- Enter "15_25_100"
Press Enter or click OK
You may use whatever name you like for these runs, BUT the name will be used as part of the filename of several files, so please do not include spaces or special characters other than "_","-" or "+" in the name. You may also consider keeping the name relatively short.
Depending on the version you are running, you may see various warning messages appear in the console after creating your new run. These can be safely ignored if present. You should see an entry for your newly created run appear in the box shown under Step 2. Make sure this new entry is selected.
Step 3
In Step 3 we create the neutral Gaussian representation for our neutral map. The "neutral map" represents the solved structure from the folder selected in step 1. It's the map produced when you include all or most of the particles in the data set, and should be a sort of average structure for the system. When we look for dynamics/variability, it will be with respect to this neutral map.
To proceed with the GMM, we need to have a Gaussian model for this neutral map. This can be generated automatically, but the user needs to provide two key parameters: 1) the level of detail at which to make the representation and 2) how strong densities need to be to be included in the representation. Item 1) is defined as a resolution (in Å), but do not confuse this with the resolution you might achieve in final classified maps. This number defines the resolution level at which variability will be studied. If you specify 30 Å here, it will be looking for changes/motions in features with a 30 Å lengthscale, but successfully isolating a more self-consistent set of particles could still readily achieve near atomic resolution maps. When starting with a new project we suggest beginning with 20-30 Å here, then if no useful variability is detected, or when you are ready to look for finer motions, then reduce the number incrementally by ~2x. You will want to make a new run (step 2) each time you try new parameters.
Item 2) specifies a relative amplitude threshold for Gaussian modeling. This is specified as a resolution-dependent threshold. Larger values -> fewer Gaussians. If there are highly dynamic regions of the structure, specifying too high a threshold may fail to produce any Gaussians in these weaker regions of the map, which will make them less likely to be characterized when training the GMM. Still, there is a balance, as a very large number of Gaussians may be difficult to train, will make the GMM run for a long time, and make the results more difficult to interpret. We suggest selecting a threshold value to produce the fewest Gaussians which seem to include at least some representation of all regions of the map.
Resolution -> 15
(box below Resolution) -> 0.5,0.7
press Resolution
You should see your neutral map shown in the panel on the right, with some number of spheres visible inside it. The number appearing below the Resolution button is the number of Gaussians in the current model. You can drag the Sphere Size slider to adjust the visual size of the spheres. This has no impact on any computations, it is purely for visualization.
There is one additional complexity. In addition to producing Gaussians representing the strongest densities in the map, a smaller number of Gaussians representing the strongest negative features in the map (relative to the solvent) will also be produced. These are generally placed in residual CTF artifacts or otherwise just outside the structure, and are useful in accurately characterizing individual particles. If (box below Resolution) is specified as a single value, a reasonable automatic value is selected for the negative threshold. Optionally, (box below resolution) can be specified as a comma-separated pair, with the first number as the threshold for positive Gaussians and the second number for negative Gaussians. If the second value is larger, fewer negative Gaussians will be created. If you look at the console after pressing Resolution, you should see an output like "pos: 244", "neg: 38", indicating that the model has 192 positive Gaussians and 46 negative Gaussians.
You can play with the parameters above and press Resolution again as many times as you like to achieve a representation you are happy with, but note that large numbers of Gaussians (>1000) may significantly increase the amount of time required to train the GMM and will increase the GPU memory requirements for the network, and in most cases won't actually accomplish anything useful, unless you are using a large number of latent dimensions. Indeed, useful results can sometimes be obtained with as few as 20 - 30 Gaussians. A few hundred is a reasonable target for typical projects.
Once the neutral Gaussian model has been defined, the neural network needs to be initialized. It's critical that the network initialization use parameters compatible with the final GMM training, so we fill these in now:
Input Res -> 25,150
Mask -> nothing, clear the box
Latent Dim -> 4
Train Iter -> 30
Model Reg -> 0
Model Perturb -> 0.25
Position -> selected
Amplitude -> selected
Press Train Neutral
A number of these parameters can actually be altered for the actual dynamics run, the ones which absolutely cannot be changed without rerunning Train Neutral are: Latent Dim, Mask and the selection state of Position and Amplitude. If you change any of these, you will need to repeat all of Step 3 before Train GMM.
Step 4
We are now on to the actual network training, where the network learns the variabilities present in the system and tries to establish a reduced dimensionality model covering the most important variations among the data.
Unlike linear methods like principal component analysis or normal modes, the model changes represented by different axes in latent space can be quite complicated and the axes are not orthogonal in any meaningful way. That is simply to say that a 4-D latent space can potentially represent far more structural variation than 4-D PCA analysis.
For runs using >100,000 particles at typical 10-20 Å resolutions, or smaller numbers of particles at higher resolutions, the particle data itself can require too much memory to train the network all at once. The # Ptcl Batches field selects how many batches to divide the particle data into for training. Breaking the data into batches requires a certain amount of additional overhead, and total runtime for training the network may be significantly longer than if run as a single batch. A reasonable value will be filled in automatically based on the number of particles in the project, but if you are targeting high resolution variations, and get error messages about memory exhaustion when trying to train the network, increasing the number of batches is a quick way to reduce memory requirements. Conversely if you have a setup with 48 GB of GPU RAM on one effective GPU, you may be able to decrease the number of batches to 1 for larger projects.
press Train GMM (New Dynamics in older snapshots)
- How long this takes to run will depend on quite a few parameters, including the number of particles (for tomographic data, think number of particles*number of tilts), number of Gaussians, Training Iterations, speed of GPU, etc. You can monitor progress in the console. Note that the main refinement program will be run 3*batches times.
Step 5
When the GMM finishes training (may be 20 minutes or hours), a scatter plot should appear in the central panel on the display. The GMM will convert each particle image in the data set into a point in the N dimensional latent space (we selected 3 dimensions above, but 4 or 5 would be more typical). In turn, each point in the latent space represents a complete 3-D configuration of the GMM. That is to say, that ostensibly, each particle now has a complete 3-D representation in terms of Gaussians. In reality, since the particles are quite noisy, the individual particles will not be positioned at exactly the optimal point in the latent space, but if we take a set of particles and average their latent space coordinates, the resulting Gaussian model should be a good match for the 3-D reconstruction which would be produced from the corresponding particles.
Again, it is difficult to represent 4 or 5 dimensional points in a useful way on 2-D plot window in the middle of the display. The simplest approach is used here, the plot will show a 2-D projection of the N-dim latent space. Using X Col and Y Col you can select which dimensions correspond to the X and Y axes in the plot. Furthermore, the program automatically runs PCA on the latent space as soon as the run is complete, and axes 0 and 1 (the default axes shown in the plot) represent a projection defined by the first 2 Eigenvectors of the PCA. Columns 2-N+1 contain the raw latent space axes. It is also possible through external programs to perform other dimensionality reduction algorithms and include the transformed coordinates as additional columns in the plot (advanced topic for later).
Dragging the mouse around in the latent space will show crosshairs with a circle. All of the points within the circle will be used to compute the Latent space location, which will then be used to update the pattern of Gaussians in the window on the right in real-time. The box to the left of Explore controls the radius of the circle. Note again, that the 2-D plot is showing a projection of an N-dimensional space, and any other dimensions will be unconstrained as you drag. ie - you are not extracting points within a 2-D circle, but an N-D hyperslab.
The 3-D view on the right can display quite a few different things. The panel of toggle buttons: Neutral Map, Neutral Model, Dynamic Map, Dynamic Model, Mask, gives one way to turn on and off the various components of the display. As usual you can also middle click on the display to open it's control panel and alter the display that way. Note that you can develop some synchronization issues between the various buttons when doing this, so sometimes you may need to turn an item off then on again or vice-versa to get things in sync again.
Turn off Neutral Map and Neutral Model. Make sure Dynamic Model is enabled. You don't have any Dynamic Maps yet, so that doesn't matter.
- Drag your mouse around the plot and observe changes.
Change X Col and Y Col and observe the different projections.
- By rotating the 3-D view you should be able to identify how specific Gaussian motions relate to specific features in the latent space.
Step 6
The next step is to generate maps from subsets of the particles. While these sets can be generated with the mouse, the resulting hyperslabs aren't generally as interesting as classes resulting from N-dim classification.
Sets -> 8
Axes -> 2-5 (make sure you don't use numbers outside the range of available dimensions, remember 0,1 are a PCA projection)
press Kmeans
You should see a list of 8 entries appear in the table below the 3-D view. Clicking on any one of these entries will highlight the corresponding points (again, each point represents a particle) and update the Gaussian model for those points. You can alter X Col and Y Col to observe that this classification is truly N-dimensional, not limited to a particular plane. You can select multiple entries at once, and each will be displayed in a different color. Note that the point size in the plot is increased when doing this to make classes easier to see.
- Select all of the sets in the list by dragging
Press Quick Map or Build Map
Build Map will perform a 3-D reconstruction for all of the particles in each selected set. Quick Map does the same thing, but downsamples the data by 2x first, making the process run about 8x faster, but limiting the maximum resolution of the map. The reconstructions are performed in the background using multiple threads (look at the console to monitor progress). As each reconstruction completes, the table will be updated. Note that the maps are reconstructed simultaneously, so if you reconstruct 20 maps at the same time, and each map is, say, 512 x 512 x 512, it may use ~20 GB of RAM. Quick Map will use 1/8 as much, and reducing the number of reconstructions you do simultaneously will also reduce requirements.
Once done, selecting one of the sets in the list will now also display the corresponding map in the 3-D view (the Dynamic Map).
- Furthermore, a central section of the map will be shown in a new window appearing in the lower right side of the display.
The thickness and center of this section can be adjusted with Thk: and Cen:.
- The orientation of the section follows the orientation of the 3-D view.
- Try switching between different sets in different orientations to observe the corresponding differences in 3-D and 2-D.
Improving results
Notes on training parameters:
Input Res - This specifies the resolution range which is used to convert individual particles into a set of Gaussian amplitudes. The second number is optional, and if not specified, the full low resolution data is included. Since SSNR is lower at higher resolution, including high resolution in this calculation may lead to each particle being 'noisier' resulting in a less precise position in the latent space. Usually the learned dynamics of the system will still be fine, but it will be hard to relate observed dynamics back to distributions of individual particles. Even relatively small motions will often be measurable at significantly lower resolutions. For example if a domain moves cohesively by only 10 Å, this will still be observable as a change in intensity at 25 Å. So, if you train the GMM and find that significant motions have been identified, but the pattern of particles in latent space (see step 4) seems to be featureless, you may consider increasing the first number. If the GMM seems to be focusing on things like ice gradients or other unimportant very low resolution features, decreasing the second parameter may be worthwhile.
Mask - Note that we are still considering other ways to handle this parameter, so its behavior may change in future versions. The Mask parameter allows you to focus the variability analysis on Gaussians within a masked region. The remaining Gaussians will still be present in the model, but will be fixed. When exploring the latent space, only the Gaussians in the masked region should change. However, when generating 3-D reconstructions from the corresponding particles any other coordinated motions should also be observed. Note that masks do not have to be fully connected, so this should be usable to look for coordinated changes between specific disconnected domains.
Latent Dim - As explained above, there is not a direct relationship between the number of dimensions in the latent space and the 'features' in the model due to the nonlinearity of the network. For looking at the overall motions of most systems 4 is a good choice. While reducing this to 2 or 3 makes visualization easier, and might be an alternative to later dimensional reduction steps, it may also make the network more difficult to train by being too restrictive.
Train Iter - This may require some trial and error, but generally something between 20 and 100 is a good choice. Note that runtimes will scale linearly with this parameter. In deep learning terms this is the number of 'epochs'. In many cases good convergence can be achieved after 20-30, but if good results are not being obtained, experimenting with larger values may be a good idea. At present, there is no way to continue an existing training session in the GUI, but this may be added soon (so insufficient training can be picked up where it left off).
Model Reg - If the training seems to drift too far from the starting model due to high noise levels, this regularizer can reduce this phenomenon with a weak restoring force towards the neutral model. If used, suggested values to try might be 0.1 - 0.2.
Model Perturb - The network training needs to be seeded with a certain amount of entropy to train well in most cases. Larger perturbations will lead to less ordering in the latent space patterns. Usually you would like this value to be as small as possible as long as good training results are achieved. The default value of 0.05 will work well in many cases, but with subtomogram averaging, sometimes stronger perturbations will be required. Generally this number shouldn't be larger than ~0.3, with 1.0 as an absolute maximum.
